Objectives: :
- – Define arithmetic sequences and series.
- – Use of the formulae for the nth term and the sum of the first n terms of the sequence.
- – Use of sigma notation for sums of arithmetic sequences.
SEQUENCE
A sequence is just an ordered list of numbers (terms in a definite order). For example :
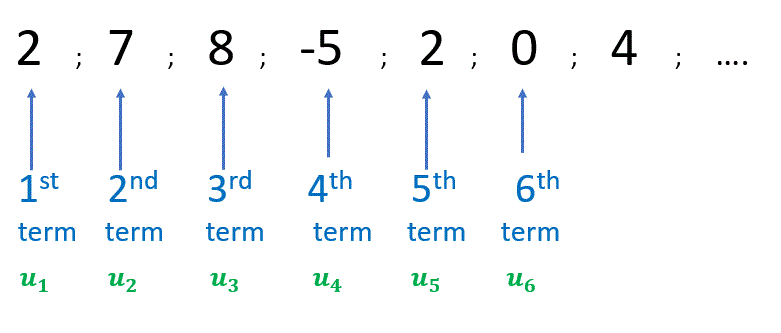
Usually, the terms of a sequence follow a specific pattern, for example
\(0,2,4,6,8,10,…\) (even numbers, \(u_n=2n-2; n \in\mathbb{N}^{*} \))
\(1,3,5,7,9,11,…\) (odd numbers, \(u_n=2n-1; n \in\mathbb{N}^{*} \))
\(5,10,15,20,25,…\) (positive multiples of 5, \(u_n=5n; n \in\mathbb{N}^{*} \))
\(2,4,8,16,32,…\) (powers of 2, \(u_n=2^n; n \in\mathbb{N}^{*} \))
We use the notation un to describe the \(n^{th}\) term. Thus, the terms of the sequence are denoted by
\( u_{1} ; u_{2} ; u_{3} ; u_{4} ; u_{5} ; …\)
SERIES
A series is just a sum of terms:
\(S_{\color{blue}{n}}=u_{1}+u_{2}+u_{3}+…+u_{\color{blue}{n}}\) : The sum of the firts n terms
\(S_{\color{green}{∞}}=u_{1}+u_{2}+u_{3}+\color{green}{…}\) : The sum of all terms
We say that \(S_{∞}\) is an infinite series, while the finite sums \(S_{1}\), \(S_{2}\), \(S_{3}\),…are called partial sums.
Example :
Consider the sequence of odd numbers :
\(1,3,5,7,9,11,…\)
Some of the terms are the following
\(u_1 =1\), \( u_2=3\), \( u_3 =5\), \(u_6 =11\), \(u_{10} =19\)
Also,
\(S_1 =1\),
\(S_2 =1+3=4\),
\(S_3=1+3+5=9\),
\(S_4 =1+3+5+7=16\)
Finally,
\(S_∞ =1+3+5+7 +…\)
SIGMA NOTATION \(\sum\limits_{n=1}^{k}\)
Instead of writing :
\(u_{\color{red}{1}}+ u_2 + u_3 + u_4 + u_5 +u_6 +u_{\color{green}{7}} \)
We may write :
\(\sum\limits_{n=\color{red}{1}}^{\color{green}{7}}u_n\)
It stands for the sum of all terms \(u_n\) , where \(n\) ranges from 1 to 7.
In general,
\(\sum\limits_{n=1}^{k}u_n\)
expresses the sum of all terms \(u_n\) , where \(n\) ranges from 1 to k.
We may also start with another value for \(n\), instead of 1, e.g. \(\sum\limits_{n=4}^{11}u_n\)
Examples :
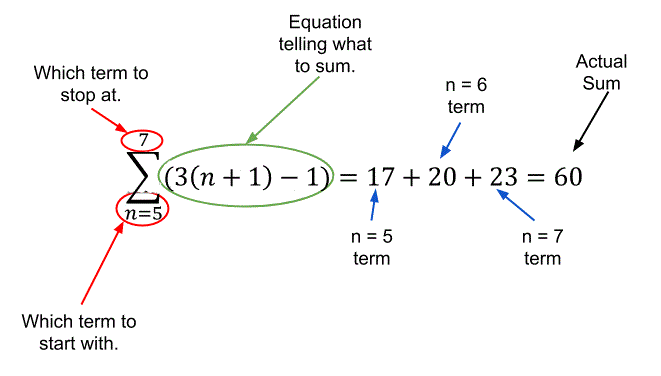
\(\sum\limits_{n=1}^{3}2^n=2^1+2^2+2^3=2+4+8=14\)
\(\sum\limits_{k=3}^{6}(2k+1)=7+9+11+13=40\)
NOTICE
There are two basic ways to describe a sequence
A) by a GENERAL FORMULA
We just describe the general term \(u_n\) in terms of \(n\).
For example, \(u_n= 2n\)
It is the sequence \( 2,4,6,8,10,… \)
(It gives \(u_1 = 2; u_2= 4; u_3 = 6; … \))
B) by a RECURSIVE RELATION (mainly for Math HL)
Given: \(u_1\) ,
the first term \(u_{n+1}\) in terms of \( u_n\)
For example,
\(u_1 = 7\)
\(u_{n+1} = u_n + 2\)
This says that the first term is 7 and then
\(u_2 = u_1 +2\)
\(u_3 = u_2 +2\)
\(u_4 = u_3 +2 \) and so on.
In simple words, begin with 10 and keep adding 2 in order to find the following term.
It is the sequence \(7, 9, 11, 13, 15, …\)
Definition:
Arithmetic sequences are characterized by the fact that to get from one term to the next we always add the same amount.
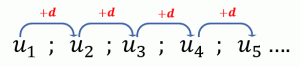
The amount we add is known as the common difference and is usually referred to as d, \( d \in \mathbb{R}\)
For example :
The sequence whose first few terms are:
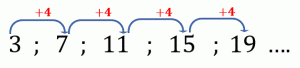 is arithmetic, with common difference \( d=4 \)
is arithmetic, with common difference \( d=4 \)
So, we need two numbers to find the others terms
The first term \( u_1 \)
The common difference \(d\)
Examples :
If \( u_1 =1, d=2\) the sequence is \(1 ; 3 ; 5 ; 7 ; 9 ; …\)
If \( u_1 =-10, d=5\) the sequence is \(-10 ; -5 ; 0 ; 5 ; 10 ; …\)
If \( u_1 =10, d=-3\) the sequence is \(10 ; 7 ; 4 ; 1 ; -2 ; …\)
![]()
What is the general formula for \(u_n\) ?
Let us think: In order to find \( u_3\) , we start from \(u_1\) and then add 2 times the difference \(d\). \(u_{\color{orange}{3}}=u_1+\color{orange}{2}d\) 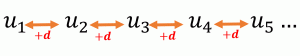 Hence,
Hence,
\(u_{\color{orange}{4}} = u_1+\color{orange}{ 3}d\)
\(u_{\color{orange}{5}} = u_1+ \color{orange}{4}d\)
Similarly,
\(u_{\color{orange}{10}} = u_1+ \color{orange}{9}d\)
\(u_{\color{orange}{50}} = u_1+ \color{orange}{49}d\)
In general,
\(u_n = u_1+ (n-1)d\)
The nth term of an arithmetic sequence is given by:
\(a_n=a_1+(n−1)d\)
where \(a_1\) is the first term and \(d\) the common difference.
Gauss Problem
|
|
In elementary school in the late 1700’s, Gauss was asked to find the sum of the numbers from 1 to 100. The question was assigned as “busy work” by the teacher, but Gauss found the answer rather quickly by discovering a pattern.\(1+2+3+4+5+6+ ….+97+98+99+100 = ? \) |
The answer is 5050. How can you do it without a calculator in a matter of minutes like Gauss?
The sum \(S_n\) of the first \(n\) terms of an arithmetic sequence is given by :
\(S_n=(u_1+u_n)\times \frac{n}{2}\)
\(S_n= (2u_1+ (n-1)d)\times\frac{n}{2}\)
\( u_1\) is the first term,
\(u_n\) the last term,
\(d\), the common difference.
Quizizz as a warm up or at the end of your course. This resource can be used by the students themselves by clicking on the “practice” button:
– Arithmetic sequence : definition and common difference– Arithmetic sequence : formula– Arithmetic series– test |
 |

