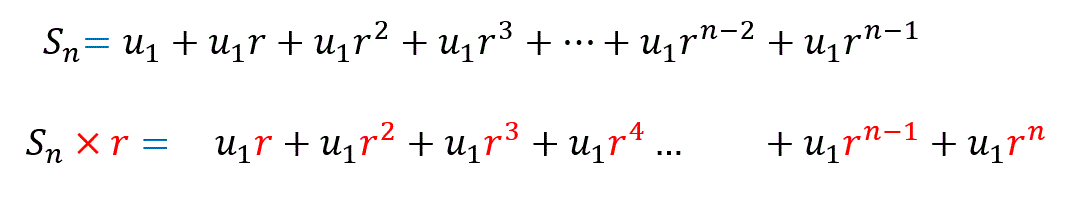- – Find the next term of a geometric sequence.
- – Find the sum of a geometric sequence.
This is an ancient legend told across Asia. A Sultan wanted to reward his servant for an act of extraordinary bravery. he told the wise man that he could choose anything for a reward. The wise man then pointed to the chessboard and asked just for a few grains of wheat in the following manner: 1 grain of wheat for the first chess square, 2 grains of wheat for the second square, 4 grains of wheat for the third square, 8 grains of wheat for the fourth square, and and carry on doubling this number on every consequent square to fill up all 64 squares of the chessboard.
The Sultan replied : “This sounds like a small price to pay for your act of incredible bravery, I will ask my servants to do as you ask immediately.”
Did the Sultan manage to fulfil the wise man’s request?
How many grains of rice did the servant have to place on the 3rd square?
How many grains of rice did the servant have to place on the 4th square?
How many grains of rice did the servant have to place on the 64th square?

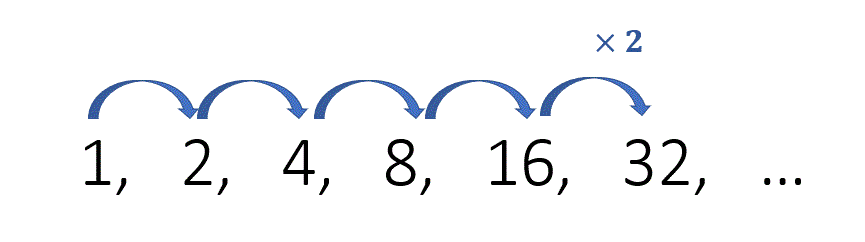
Can you see the pattern ? Each time we are multiplying by 2.
On the second square there is 2 grains
On the \(3^{rd}\) square : \(2\color{blue}{\times 2} = 2^{2}\)
On the \(4^{th}\) : \( 2^{2} \color{blue}{\times 2} = 2^{3}\)
On the \(64^{th}\) square : \( 2^{63}\). This is \( 9.223 \times 10^{18}\) grains of wheat or about \(9, 223, 372, 037, 000, 000, 000\) grains of wheat !
Definition:
A geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio.
For example, the sequence 2, 6, 18, 54, … is a geometric progression with common ratio 3.
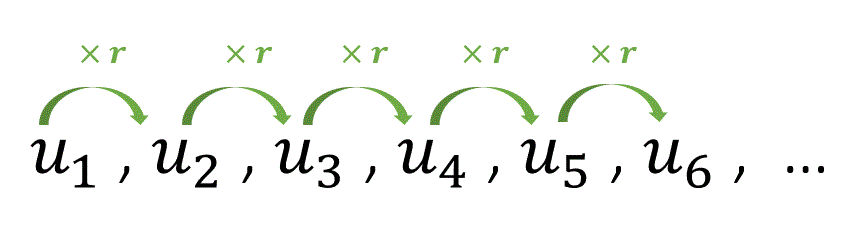
\(u_{1}\) is the first tem and \(r\), the common ratio. We only need both of them to describe a geometric sequence.
Exemple :
-
\(u_{1} =5 , r = 10\) the sequence is: 5, 50, 500, 5000, …
-
\(u_{1} =1, r = -2\) the sequence is: 1,-2, 4,-8, 16, …
Exercise : Multiple choice
Exercise :
In order to find \(u_{5}\), we start from \(u_{1}\) and then multiply 4 times by the ratio \( r\).
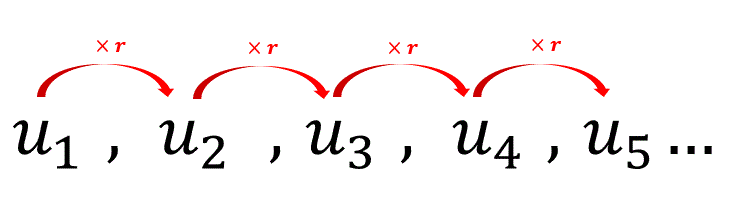
Hence \( u_5=u_1\times r^{4}\)
Similarly \( u_{20}=u_1\times r^{19}\) and \( u_{100}=u_1\times r^{99}\)
The n-th term of a geometric sequence with initial value \( u_1\) and common ratio \(r\) is given by
\( u_n=u_1\times r^{n-1}\)
Exercise
Exercise
Exercise
Exercise

Think again about the chessboard problem. We already know what a huge amount of rice must be placed on the last square. But how much rice has to be placed in total on the board?
\(S_{64}=u_1+u_2+u_3+u_4+…+u_{62}+u_{63}+u_{64}\)
using the general forumula :
\(S_{64}=u_1r^0+u_1r^1+u_1r^2+u_1r^3+…+u_{1}r^{61}+u_{1}r^{62}+u_{1}r^{63}\)
The sum \(S_n\) of the first \(n\) terms :
\( S_n=u_1+u_1r^1+u_1r^2+…+u_{1}r^{n-2}+u_{1}r^{n-1}\)
is given by (\( r \neq 1\)) :
\(S_n=\frac{u_1(r^n-1)}{r-1}\) or \(S_n=\frac{u_1(1- r^n)}{1-r}\)
Proof
By definition :
We substract theses two expressions :
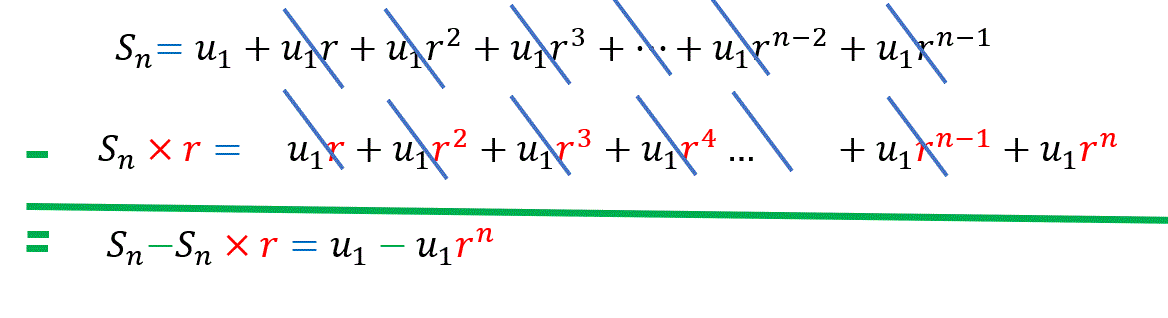
then,
\(S_n(1-r)=u_1(1-r^n)\)
\(S_n=\frac{u_1(1-r^n)}{1-r}\)
Example:
Consider the sum:
\( 2+2^2+2^3+2^4+…+2^10\)
It is a geometric series of 10 terms with \(u-1 =2 \) and \( r =2 \)
Hence, the sum is:
\(S_{10}=\frac{2(1-2^{10})}{1-2}=2046\)
Exercise :
The sum of ∞ terms in a geometric sequence
Consider the sum of the infinite geometric sequence
\(S_∞ = u_1 + u_2 + u_3 +………\) (it never stops!)
The result exists only if \( -1< r <1 \). It is given by the formula
\( S_∞=\frac{u_1}{1-r}\)
In this case we say that the series converges.Otherwise (that is if\( |r|>1\) ) we say that the series diverges.
Proof
Consider the formula for \(S_n\) :
\(S_n=\frac{u_1(1-r^n)}{1-r}\)
If \(n→∞\) (i.e. n tends to infinity) then \(r^n → 0\) (\(since -1< r <1\))
and \(S_n→\frac{u_1(1-0)}{1-r}=\frac{u_1}{1-r}\)
Example :
Show that :
\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+…… =1 \)
Solution :
This is an infinite geometric sequence with \(u_1=\frac{1}{2}\) and \(r=\frac{1}{2}\)
Since \(|r|<1\) we obtain:
\(S_∞ = \frac{u_1}{1-r}=\frac{\frac{1}{2}}{1-\frac{1}{2}}=\frac{\frac{1}{2}}{\frac{1}{2}}=1\)
Exercise