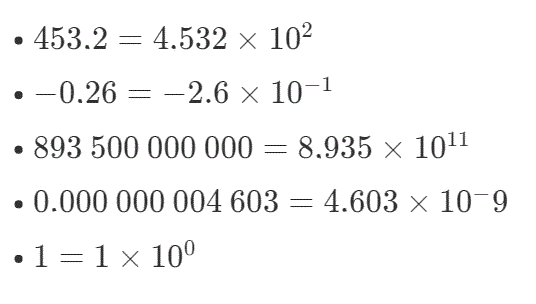SL 1.1 Standard form

Objectives:
:

  • – Express large and small numbers in scientific notation.
  • – Use your GDC (Graphic Display Calculator) to find numbers in scientific notation.

Consider the number:

123.4567

 
There are two ways to round up the number by using fewer digits:
1. In a specific number of decimal places (d.p.)

in 1 d.p. 123.5
in 2 d.p. 123.46
in 3 d.p. 123.457

2. In a specific number of significant figures (s.f.). For the position of cutting we start counting from the first non-zero digit:

in 4 s.f. 123.5in 5 s.f. 123.46
Inchangé : in 6 s.f. 123.457

But also

in 2 s.f. 120
Inchangé : in 1 s.f. 100

 

Important remark: In the final IB exams the requirement is to giveInchangé : the answers either in exact form or in 3 s.f.

For example:

\(2\pi\)6.28

Exact form in 3 s.f.
\(\sqrt{2}\) 1.41
12348 12300

METHOD:

The method is the same as with decimal places except that you start counting from theInchangé : very beginning of the number (instead of just after the decimal point):

– If 5 or above then round the last number up.

– If 4 or below the last number stays the same

Examples:

a. Round 15.748 to 3 significant figures.

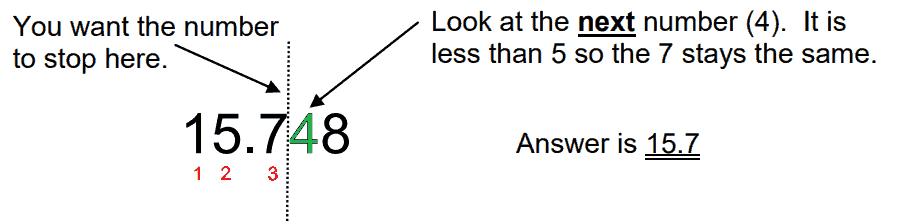
b. Round 64.3463 to 2 significant figures.

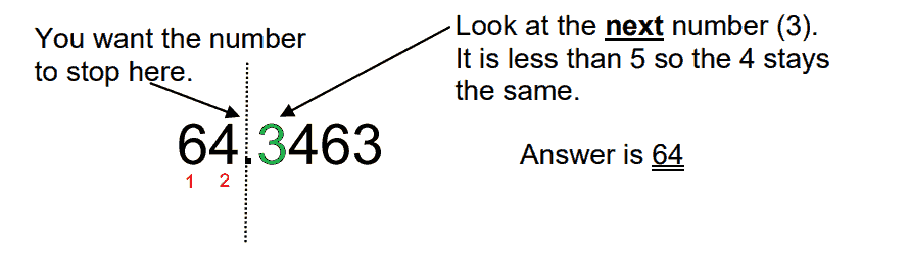
c. Round 128.35 to 2 significant figures.

 

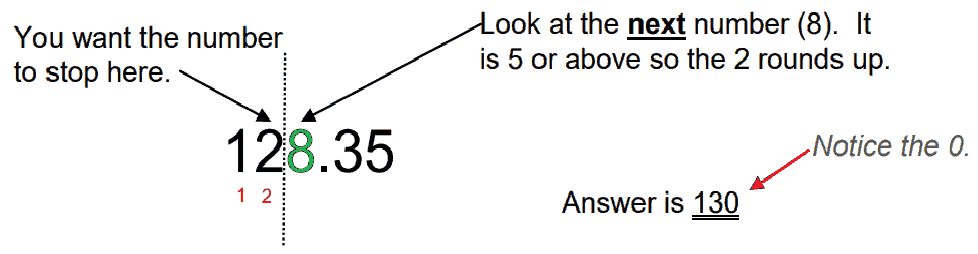
Exercise

 

Find each of these values as a power of 10.

Example : 1 000 = 103

   

 

  Find each of these values as a power of 10.

Example : 0.001 = 10-3

 

 

Reminder

For a positive integer n :

  • \(10^{\color{red}{n}}\) is written with a 1 followed by n zeros.
  • \(10^{\color{green}{-n}}\) is written with a 1 preceded by n zeros.

 

 

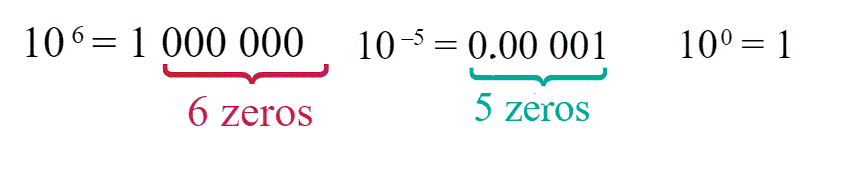
Exercise :

 

answer the question writing the letter, like this : \(s=2\)

 

 

How can we use our findings so far to express numbers as multiple of powers of ten .

For example \( 8, 000\) :

\( 8, 000 = 8 \times 1,\color{green}{000} \) and we know\( 1, \color{green}{000} = 10^{\color{green}{3}}\)

so, \( 8, \color{green}{000} = 8\times10^{\color{green}{3}}\)

what about \( 60 ,000 ,000 \) ?

\( 6\color{green}{0, 000 ,000 }= 6\times 1\color{green}{0 ,000 ,000}\)

\( 6\color{green}{0, 000, 000}= 6\times 10^{\color{green}{7}}\)

and \( 0.005 \)?

\(\color{red}{ 0.00}5=5\times \color{red}{ 0.00}1\)

\(\color{red}{ 0.00}5=5\times 10^{\color{red}{ -3}}\)

 

Match all these numbers with their form in \(a\times 10^{k}\) where \( k \in \mathbb{Z}\)

 

Exercise

 

Scientific Notation

 

Any number can written in the form :

\( a \times 10^k\) where \( 1 \leq a<10 \) and \( k\in \mathbb{Z}\)

 

 

Scientific notation is a standard way of writing very large and very small numbers so that they’re easier to both compare and use in computations.

 

Examples :

METHOD:

 

Write 427 000 000 000 in scientific notation:

  1. Move the decimal place to the left to create a new number from 1 up to 10. Inchangé :
    • The decimal point is at the end of the number:
    • 427 000 000 000. So, \(a=4\color{red}{.}27\)
  2. Determine the exponent, which is the number of times you moved the decimal point.
    • In this example, you moved the decimal 11 times; also, because you moved the decimal to the left, the exponent is positive. Therefore, k = 11, and so you get \( 10^{11}\)
  3. Put the number in the correct form for scientific notation
    • \( a \times 10^{k}\)
    • \(4.27\times10^{11}\)

Write 0.00 000 037 in scientific notation.

  1. Move the decimal place to the right to create a new number from 1 up to 10.
    • So \( a=3\color{green}{.}7\)
  2. Determine the exponent, which is the number of times you moved the decimal point.
    • In this example, you moved the decimal 7 times; also, because you moved the decimal to the right, the exponent is negative. Therefore, \(a = –7\), and so you get \(10^{-7}\)
  3. Put the number in the correct form for scientific notation
    • \( a \times 10^k\)
    • \(3.7\times10^{-7}\)

 

 

 

Exercise – Level 🔅

 

Exercise – Level 🔅🔅

Exercise – Level 🔅🔅🔅

Exercise – Level 🔅🔅🔅🔅

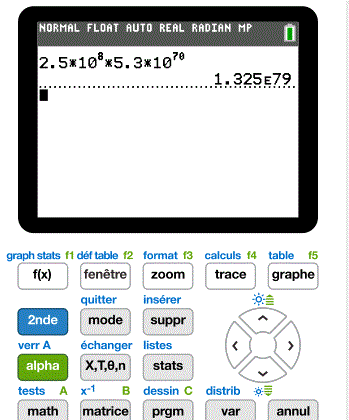
Most calculators use the symbol E± for the scientific notation:

 

1.325E79 means \(1.325\times 10^{79}\)

 

Exercise :

NOTICE :

They may ask us to give the number in scientific form but also in 3 s.f. Then :

\(1.2345×10^{2}≅1.23×10^{2}\)

\(3.2045×10^{-5}≅3.20×10^{-5}\)

..

Quizizz as a warm up or at the end of your course. This resource can be used by the students themselves by clicking on the “practice” button:

– Significant figures

– Powers of 10

– Scientific notation

– Scientific notation-calculation