Multiplication tables remain a nightmare for schoolchildren to see worse for students. Emmanuel Macron knows very well this cold and terrible fear of being questioned about it, and this still currently… .
Teacher I tried to find ways to help my students better memorize these tables and create quick computational automatisms. Generally there was no concern about memorizing tables from 1 to 5, it was tables 6, 7, 8 and 9 that posed more problems.
I discovered, one day, this old technique, simple to use. But then why, as students, none of our math teachers tried to pass it on to us? …. I remain perplexed by this finding. Calculating with your fingers is the basis of the calculation… At the premise of mathematics, it was the pebbles that were used. The word calculus comes from the Latin calculus (“pebble”).
This process of multiplication is indicated in the khulasat alhissab of the author Baha’ Al-din(1547-1622). But we find it, earlier written by master Nicolas Chuquet in the Triparty in the science of numbers (1484),as well as the principle of multiplication posed still taught today in schools.
It has the advantage of retaining by heart only the products of the first integers up to \( 5times 5 \) and easily deduce the products of the other integers up to \( 9times 9 \) . In other words, this method will only be used if the two factors in the product are strictly greater than 5.
Example: Let be the product \( 8times 9 \) to be determined.
Note that \( 8 = 5+color{red}{3} \) and \( 9 = 5+color{red}{4} \)
We raise 3 doitgs with one hand and 4 with the other, the other fingers being lowered, i.e. \( 5-color{red}{3}=color{blue}{2} \) for one and \( 5-color{red}{4}=color{blue}{1} \) for the other.
The amount of fingers raised is \( 3+4=7 \) gives the figure of the product’s tens \( 8times 9 \) .
The product of the numbers corresponding to the lowered fingers is \(2 times \) 1 = 2 gives the digit of the units.
We find \( 8times 9 = color{red}{7}color{blue}{2}\)
The detailed method in video:
To go further
With students of 3rd grade, after having them discover this method, it is quite wise to ask them to demonstrate it rigorously using the literal calculation … (Challenge posed in group work, class atmosphere guaranteed!)
Proof: let \( a and b be two natural \) \( \) integers such that \( 5 , <a <10 \) \( 5 <b <10 \) .
\( atimes b = (5+c)(5+d) \) so c , d are two natural numbers such that \( \) \( \) \( 0 and <c <5 \) \( 0<d<5\)
\( = color{green}{5times 5 }+ color{red}{5c+5d}+cd\)
\(=color{green}{25}+ color{red}{10c+10d -5c-5d}+cd\)
\(=25+color{brown}{ 10c+10d} -5c-5d+cd\)
\(=color{brown}{10(c+d)}+color{blue}{25-5c-5d+cd}\)
\(=10(c+d)+color{blue}{(5-c)(5-d)}\)
Thus: \( 10(c+d): \) represents the number of fingers raised multiplied by 10.
\((5-c) (5-d) \) : the product of the numbers represented by the closed fingers
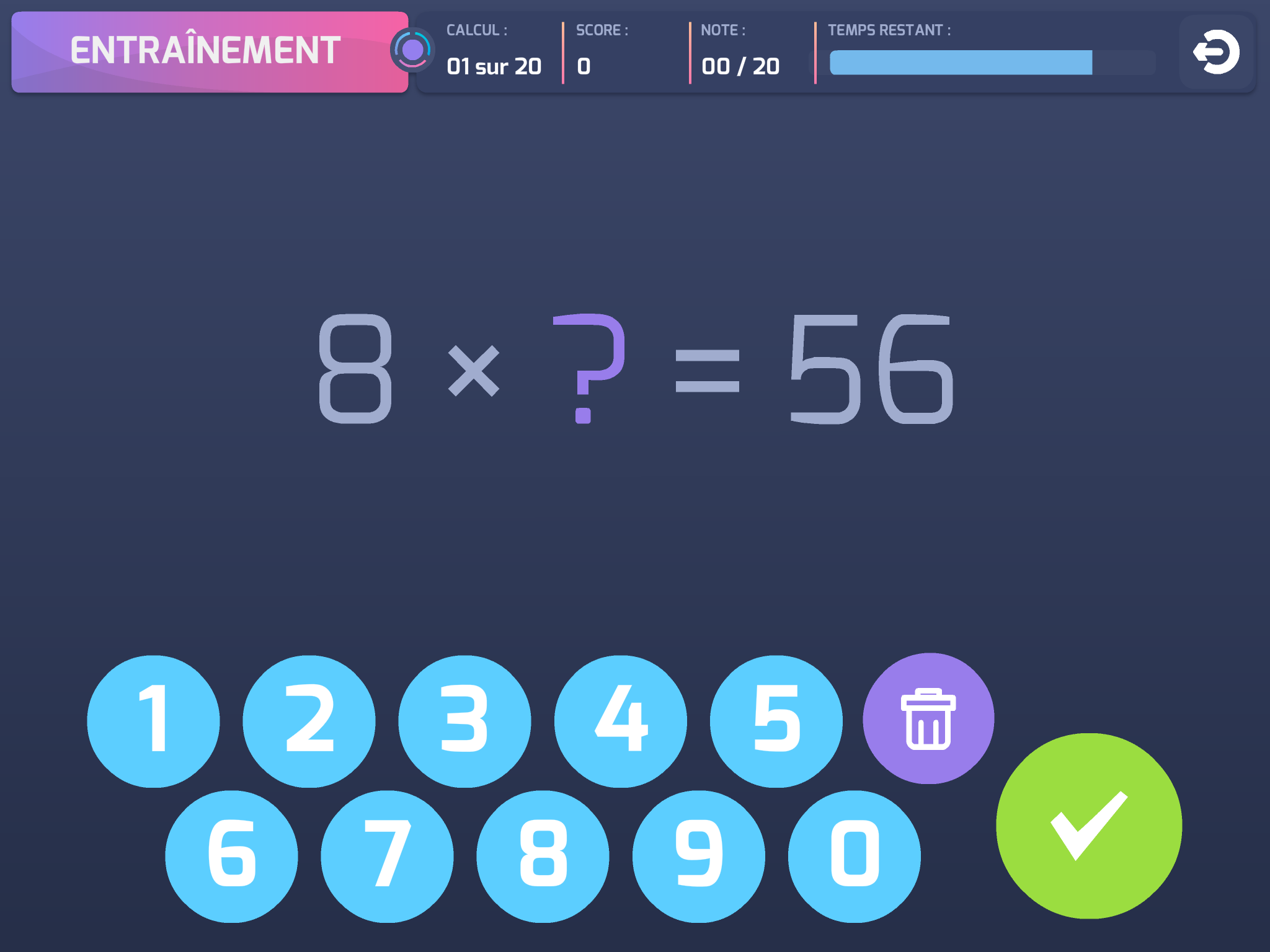
After this acquired method, it is important to work on rapidity and automatism in mental calculation using like a high-level athlete who works, every day, the same gestures to perform in his discipline …
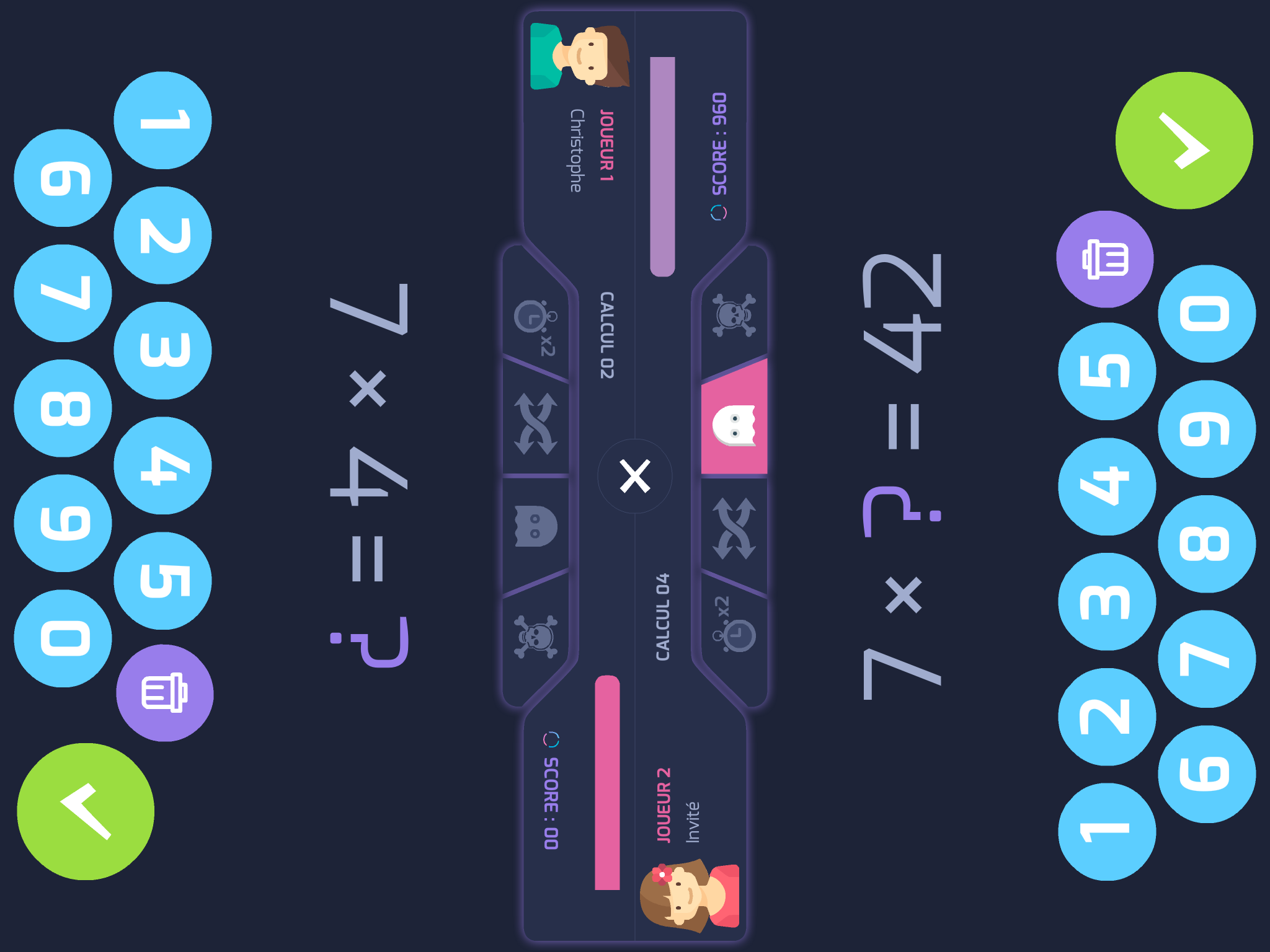
A free application (and I hope that will remain so for a good time) developed by Christophe Auclair has the gift of challenging students alone or in duo. This application combines gamification and mental calculation. Students see it as a real relaxation in class and like to challenge themselves in a variety of ways.
To download and use without moderation in class, like at home!