Se remémorer les formules d’addition en trigonométrie à l’aide du produit scalaire, ne prend que quelques secondes…
Démonstration :
Soit \( \color{red}{\overrightarrow{u}}(\cos\color{red}{a} ; \sin\color{red}{a}) \)
et \( \color{green}{\overrightarrow{v}} (\cos\color{green}{ b };\sin\color{green}{b}) \)
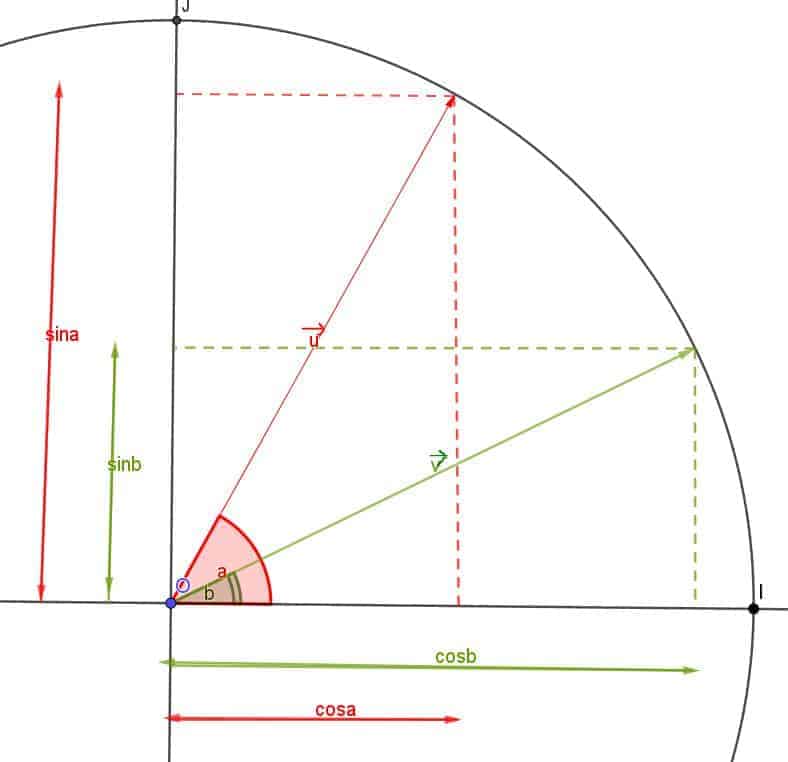
-
Par définition \( \color{red}{\overrightarrow{u}}.\color{green}{\overrightarrow{v}}= x_{\color{red}{\overrightarrow{u}}}\times x_{\color{green}{\overrightarrow{v}}} +y_{\color{red}{\overrightarrow{u}}}\times y_{\color{green}{\overrightarrow{v}}} \)
Ainsi : \( \color{red}{\overrightarrow{u}}.\color{green}{\overrightarrow{v}}= \mathbf{\cos\color{red}{ a} \cos \color{green}{b} + \sin \color{red}{a} \sin \color{green}{b}}\).
Nous avons également : \( \color{red}{\overrightarrow{u}}.\color{green}{\overrightarrow{v}}= ||\color{red}{\overrightarrow{u}}|| \times ||\color{green}{\overrightarrow{v}}|| \times \cos(\color{red}{\overrightarrow{u}};\color{green}{\overrightarrow{v}})\)
\( \color{red}{\overrightarrow{u}}.\color{green}{\overrightarrow{v}}=1 \times 1\times \cos (\color{red}{a}-\color{green}{b}) = \mathbf{\cos (\color{red}{a}-\color{green}{b})}\).
On obtient donc :
\(\mathbf{\cos (\color{red}{a}-\color{green}{b})=\cos \color{red}{a} \cos\color{green}{ b} + \sin \color{red}{a} \sin \color{green}{b}}\) \( E_1\)
-
Sachant que \(\cos (\color{red}{a}+\color{green}{b})=\cos (\color{red}{a}-(-\color{green}{b})) \). En utilisant la formule précédente on obtient :
\(\cos (\color{red}{a}+\color{green}{b})=\cos \color{red}{a} \cos (-\color{green}{b}) + \sin \color{red}{a} \sin (-\color{green}{b})\) or \( \cos (-\color{green}{b}) = \cos \color{green}{b}\) et \( \sin (-\color{green}{b}) = – \sin \color{green}{b}\).
On obtient donc :
\(\mathbf{\cos (\color{red}{a}+\color{green}{b})=\cos \color{red}{a} \cos \color{green}{b} – \sin \color{red}{a} \sin \color{green}{b}}\) \( E_2\)
-
Sachant que \(\sin (\color{red}{a}-\color{green}{b})=\cos (\frac{\pi}{2} -(\color{red}{a}-\color{green}{b})) = \cos ((\frac{\pi}{2} -\color{red}{a})+\color{green}{b}) \)
\(\sin (\color{red}{a}-\color{green}{b})=\cos (\frac{\pi}{2} – \color{red}{a}) \cos \color{green}{b} – \sin (\frac{\pi}{2} – \color{red}{a}) \sin \color{green}{b}\). En utilisant \(E_1\)
Or \(\cos ((\frac{\pi}{2} -\color{red}{a}) = \sin \color{red}{a}\) et \(\sin (\frac{\pi}{2} – \color{red}{a}) = \cos \color{red}{a}\)
d’où :
\(\mathbf{\sin (\color{red}{a}-\color{green}{b})=\sin \color{red}{a} \cos \color{green}{b} – \sin \color{green}{b} \cos \color{red}{a}}\) \( E_3\)
-
\(\sin (\color{red}{a}+\color{green}{b})=\sin (\color{red}{a}-(-\color{green}{b})) \). En utilisant la formule précédente, on obtient :
\(\sin (\color{red}{a}+\color{green}{b})=\sin \color{red}{a} \cos (-\color{green}{b}) – \sin(- \color{green}{b}) \cos \color{red}{a}\) or \( \cos (-\color{green}{b}) = \cos \color{green}{b}\) et \( \sin (-\color{green}{b})= – \sin \color{green}{b}\).
On obtient donc :
\(\mathbf{\sin (\color{red}{a}+\color{green}{b})=\sin \color{red}{a} \cos \color{green}{b} + \sin \color{green}{b} \cos \color{red}{a}}\) \( E_4\)
Ces quatres relations, alliées à celle l’équation du cercle trigonométrique :
\((\cos x)^2+( \sin x)^2=1\)
permettent facilement de retrouver la majorité des autres formules et relations trigonométriques indispensanbles au lycée et en licence. Mais voilà, rares sont les étudiants pensant à cette méthode. La majorité essaiera d’apprendre par coeur ces formules …
Voici une méthode ( certes peu rationnelle), mais elle a eu le mérite d’aider un grand nombre d’étudiants dans la mémorisation et reformulation de ces formules.
EVALUEZ-VOUS !
Pour vous évaluer vos connaissances sur l’ensemble des formules à connaitre , testez-vous ici.
[et_social_follow icon_style=”slide” icon_shape=”rounded” icons_location=”top” col_number=”auto” counts=”true” counts_num=”0″ total=”true” outer_color=”dark” network_names=”true”]
